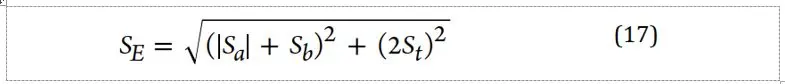Poniżej jest długi wpis. Jego zrozumienie pozwala na rozróżnienie pomiędzy zwykłym użytkownikiem programu takiego czy innego klikającym bez zrozumienia jak to działa, a inżynierem d.s. obliczeń wytrzymałości rurociągów, który ma ponadprzeciętną wiedzą jaka hipoteza leży o podstawy wytrzymałości materiałów. Jeśli należysz do tej drugiej grupy, to ten wpis jest dla ciebie.
NAPRĘŻENIA GŁÓWNE I HIPOTEZY WYTĘŻENIOWE
Wyobraźmy sobie element materiału podlegający rozciąganiu według poniższego rysunku. Płaszczyzna a – a jest skierowana pod kątem alfa do kierunku działania siły F na płaszczyznę A wytwarzając naprężenie rozciągające S. Siłę F można rozłożyć na dwie składowe: Fn – normalną i Fs – styczną do płaszczyzny a – a. Składowe te powodują naprężenia normalne sigma i styczne teta o wartościach opisanych poniższymi wzorami:
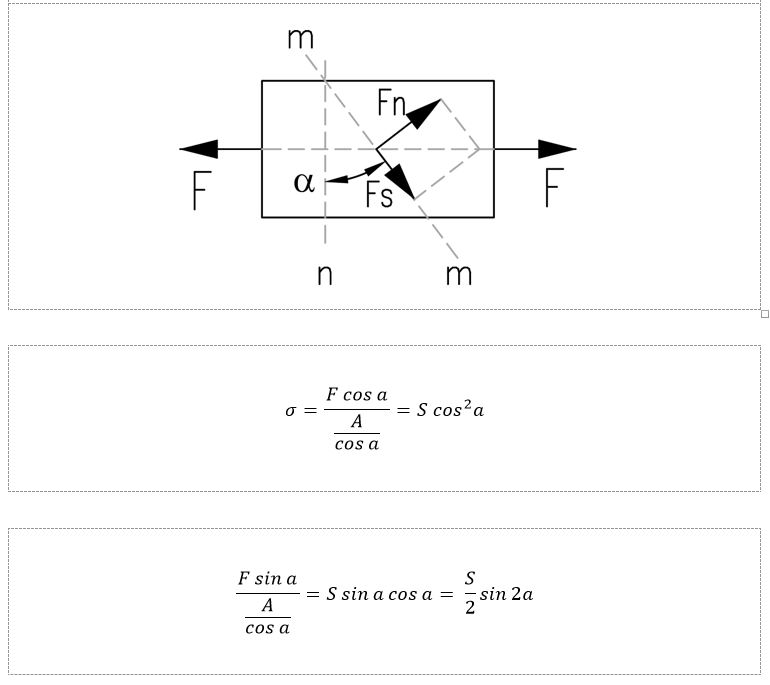
Jest oczywiste, że dla stałej wartości siły F naprężenie normalne i styczne zależą jedynie od kąta pochylenia płaszczyzny. Maksimum naprężenia stycznego teta wyniesie dla sin 2 alfa = 1 (co odpowiada kątowi a = 450) połowę wartości naprężenia rozciągającego próbkę. Maksimum naprężenia normalnego sigma wystąpi oczywiście dla kąta alfa = 00, zaś jego minimum dla kąta alfa = 900. Naprężenia w takich płaszczyznach charakteryzują się brakiem składowej stycznej i są nazwane naprężeniem głównym.
Tradycyjne naprężenia główne były wyznaczane za pomocą serii prostych konstrukcji z dziedziny geometrii analitycznej zwanych kołem Mohra, którego przykład podano poniżej.
Załóżmy, że naprężenie normalne sigmax i styczne tetaxz są większe od zera i można je pokazać w poniższym układzie współrzędnych sigma-tetea. Odkładamy wartość naprężenia normalnego sigmax na osi s, a na jego końcu wartość naprężenia stycznego tetaxz.
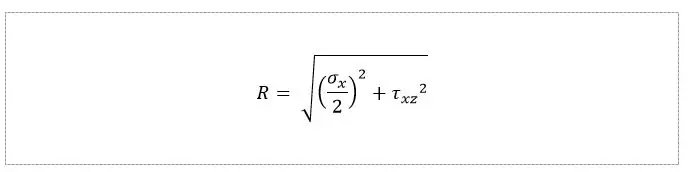
Kreślimy okrąg o promieniu R, którego początek jest w połowie wartości naprężenia normalnego sigmax. Wyznaczamy naprężenia główne maksymalne i minimalne, gdzie okrąg przecina się w punktach zerowej wartości naprężenia stycznego teta. W ostatnim kroku wyznaczamy kierunki ich działania.
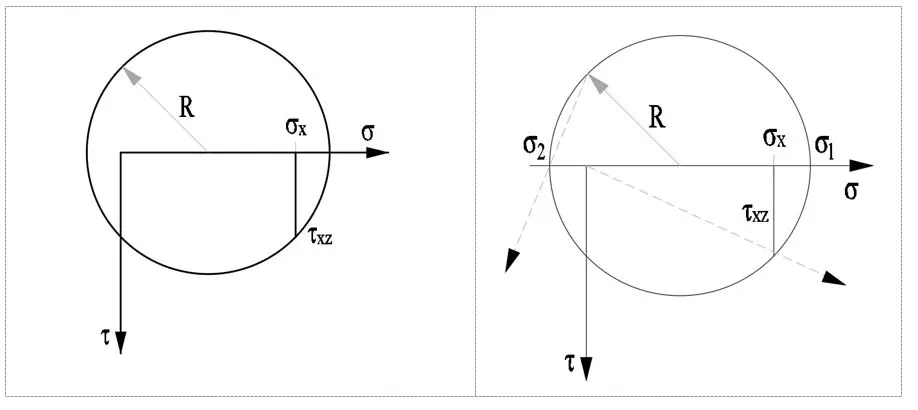
Naprężenia główne (tutaj sigma1, sigma2, sigma3) są punktem wyjścia dla dwóch hipotez używanych w obliczeniach rurociągów.
Pierwsza to hipoteza pracy właściwej odkształcenia czysto postaciowego sformułowanej i opublikowanej w 1904 roku przez wybitnego polskiego profesora M.T Hubera (1872-1950) szerzej znana, jako hipoteza R. Misesa (1883-1953), który opublikował ją dopiero dziewięć (!) lat później bo 1913 roku. Obaj pod ponowieniem tego samego władcy Franciszka Józefa I, tyle tylko, że ten pierwszy był Polakiem urodzonym w maleńkim miasteczku na Podhalu, a ten drugi w Austriakiem żyjącym stolicy Cesarstwa w Wiedniu. Czy to była kradzież stulecia, która uszła austriackiemu arystokracie na sucho trudno teraz to rozstrzygnąć. Było jednak o co walczyć bo hipoteza pracy właściwej odkształcenia czysto postaciowego, która była ukoronowaniem pracy wielu europejskich uczonych w całym XIX wieku jest tym samym, czym cztery równania Maxwella dla naszej elektromagnetycznej cywilizacji. Jest to absolutna podstawa nauki o wytrzymałości materiałów.
Postać ogólnego równania dla trójosiowego stanu naprężenia przedstawia się następująco:
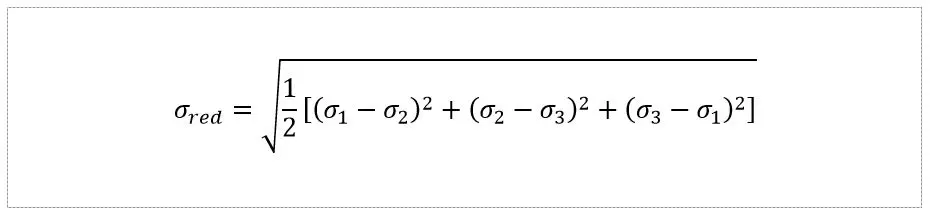
Druga hipoteza, największego naprężenia stycznego Tresca-Coloumba, która postuluje, że o wytężeniu materiału decyduje osiągnięcie przez materiał krytycznego naprężenia stycznego. Dla prostego rozciągania wartość ta wynosi połowę naprężenia rozciągającego. Dla trójosiowego stanu naprężenia wartość wytężenia wynosi:
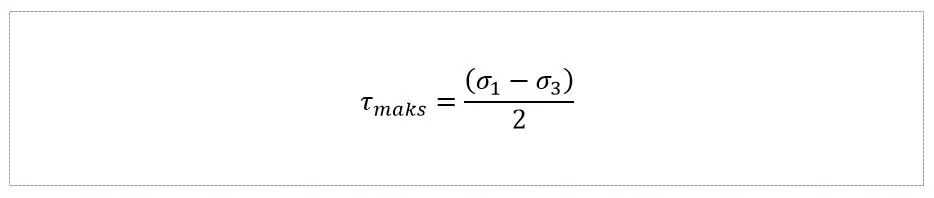
PRAKTYCZNE WYKORZYSTANIE KOŁA MOHRA
Przyjmijmy lokalny układ współrzędnych o charakterystycznych dla układu rurociągów nazewnictwie: naprężenie podłużne (naprężenie wzdłuż rury), naprężenie obwodowe (lub naprężenie obwodowe na obwodzie) i naprężenie promieniowe przechodzące przez ściankę rury. Przedstawione je na poniższym rysunku.
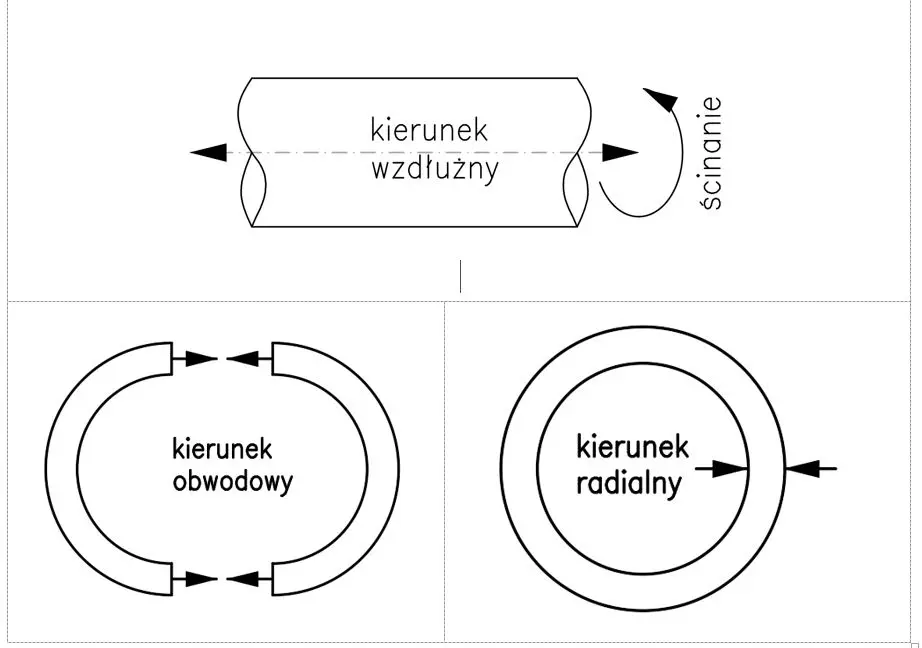
W kolejnym kroku ze ścianki rury wyodrębniono sześcian i naniesiono naprężenia główne. Mamy zatem naprężenia: podłużne sigmaL, ścinające teta , obwodowe sigmaH i promieniowe sigmaR.
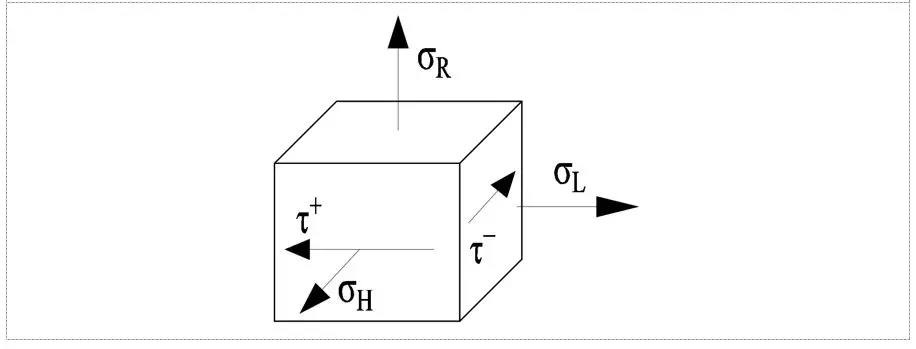
W następnym kroku określamy powyższe naprężenia, które są wynikiem przemieszczenia, głównie termicznego, a nie ciśnienia wewnętrznego:
- Wzdłużne: siła / powierzchna przekroju i/lub moment zginający / wskaźnik wytrzymałości przekroju na zginanie
- Obwodowe: do pominięcia dla cienkich ścianek
- Promieniowe: zero na powierzchni zewnętrznej
- Ścinające: siła poprzeczna / 2 x wskaźnik wytrzymałości przekroju na ścinanie.
Z powyższego zestawienia widać, że jeśli powodem jest przemieszczenie, to tylko naprężenia wzdłużne i ścinające są różne od zera, Dodatkowo są one zbilansowane, ponieważ układ pozostaje w spoczynku.
Po przecięciu płaszczyzną układ pozostaje również w równowadze. W celu wyznaczenia naprężeń w nowej płaszczyźnie może użyć konstrukcji koła Mohra.
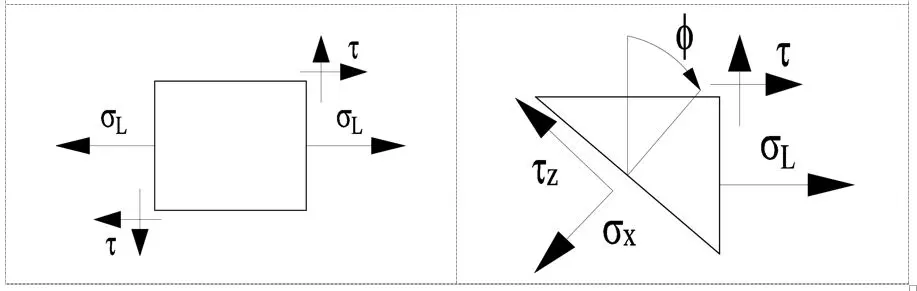
Jak wiemy naprężenie główne występują wtedy, gdy naprężenia ścinające równe są zero. Okrąg przecina oś rzędnych w dwóch takich punktach, które oznaczono parami naprężeń, w których naprężenie teta jest równe zero. Dowolny kąt fi przecięcia płaszczyzną można znaleźć z według poniższego schematu, a następnie można wyznaczyć graficznie naprężenia normalne i ścinające.
Naprężenia główne w zakresie rury obciążonej przemieszczeniem występują w trzech punktach od S1 do S3:
- S1 o największej wartości odpowiada rozciąganiu
- S2 równa się zero, co odpowiada radialnym
- S3 odpowiada ściskaniu
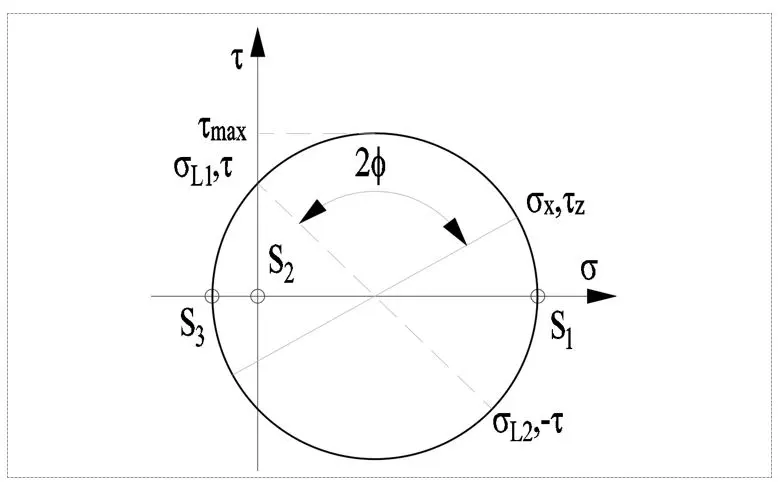
Z koła Mohra można wyznaczyć maksymalne naprężenie ścinające, którego wartość można określić prostym poniższym wzorem. W normach projektowych np. ASME B31.3 jest to granica wytrzymałości materiału.

Powyższy wzór można porównać ze znaną zależnością normową, która okazuje się, co do zasady identyczna. Temat obliczeń normowych będzie jednak rozwinięty w kolejnym wpisie.